A Multi-Layer Perceptron (MLP) is a type of artificial neural network that consists of multiple layers of nodes (perceptrons). Unlike a single-layer perceptron, an MLP has one or more hidden layers between the input and output layers. Each node in a layer is connected to every node in the subsequent layer.
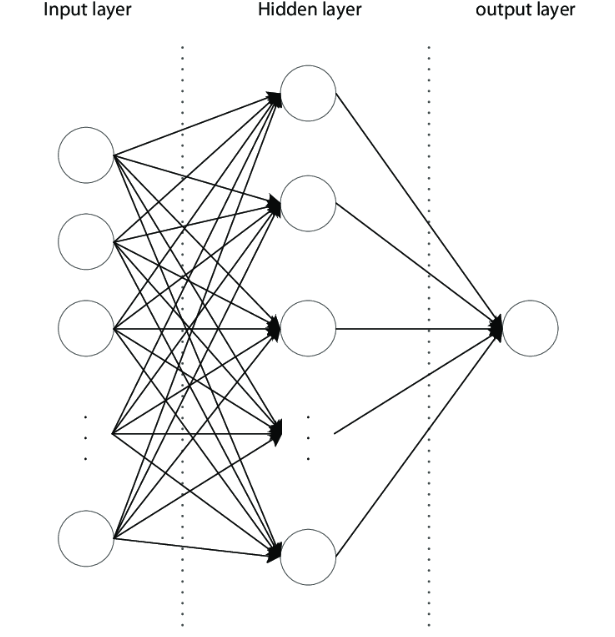
Here’s a basic overview of how an MLP works:
- Input Layer: This layer consists of nodes representing the input features. Each node corresponds to one feature of the input data.
- Hidden Layers: These are intermediate layers between the input and output layers. Each hidden layer consists of multiple nodes, and each node is connected to every node in the previous and subsequent layers. The hidden layers allow the network to learn complex patterns and relationships in the data.
- Output Layer: This layer produces the final output of the network. The number of nodes in the output layer depends on the nature of the problem (e.g., classification, regression). For example, in a binary classification task, there might be one output node representing the probability of one class, while the probability of the other class can be inferred from the complement.
- Activation Function: Each node in the hidden layers and the output layer typically applies an activation function to the weighted sum of its inputs. Common activation functions include the sigmoid function, the hyperbolic tangent function (tanh), or the rectified linear unit (ReLU) function.
- Training: MLPs are trained using supervised learning methods such as backpropagation. During training, the network adjusts the weights and biases of the connections between nodes to minimize the difference between the predicted output and the actual output. This is typically done by iteratively updating the weights using gradient descent optimization algorithms.
MLPs are versatile and can be used for various tasks, including classification, regression, and function approximation. They have been widely applied in fields such as computer vision, natural language processing, and finance. However, they can be prone to overfitting, especially when dealing with high-dimensional data or small datasets, so regularization techniques are often employed to mitigate this issue.

